Link Utili
Home Page Esempi su PlotDF e Rk Cheat Sheet Computação Matemática Elementar em Maxima Maxima@Texas[vedi Mailing List] Schelter's Home Page Syracuse Viktor's Home Page [Tensori in Maxima] Appunti dal corso di meccanica Computazionale (Spagnolo) excel2maximaAvvio
A differenza di altri software commerciali [?] maxima ha tre modalità di avvio:- Modalità Interattiva [Grafica e Testuale] $ maxima (xmaxima)
- Modalità Batch $ maxima -b file_batch
Dove "file_batch" è ovviamente un file che contiene comandi da far eseguire al programma in sequenza senza interazione [?] da parte dell'utente
Maxima restarted
un prompt di input: %i1 [al contrario gli eventuali output
saranno preceduti da %ox] attendente i nostri comandi [sul
sito leggo che in realtà le label per i prompt prima dell'ultima
versione erano Cx e Dx ma non mi pare
importante, comunque è possibile impostare i prompt tramite
inchar:label_voluta; e outchar:label_voluta;]. Maxima funziona sia da calcolatrice che da "calcolatore simbolico", ma procediamo per gradi.
Customize
Linea di Comando
Prima cosa da sapere è che i comandi devono essere terminati con un punto e virgola [;] oppure se non si vuole restituito il risultato bisogna usare come carattere di terminazione il dollaro [$]: finché non si terminano le espressioni il programma rimarrà in attesa di ulteriori input. Un computer è bravo a effettuare calcoli, ma ovviamemnte non può tenere tutte le cifre possibili in un calcolo, di conseguenza esistono delle variabili preimpostate che contengono queste informazioni.NUMER: variabile booleana che obbliga alcune funzioni [il manuale non dice quali]
con argomenti numerici ad essere esplicitate numericamente [tranne l'esponenziale].
E` anche possibile salvare e poi reloadare comandi dati durante una cosidetta sessione che magari non si vogliono perdere; per salvare si digita:
stringout(PATH,INIZIO,FINE)
Per caricarlo invece
batch(PATH);
Operazioni elementari
Le operazioni implementate in Maxima sono quelle che banalmente uno si può aspettare da una calcolatrice:+ - * / [prossimamente tabella con priorità operatori] oltre che i meno conosciuti [?]
Ovviamente esistono tutte una serie di costanti preimpostate utili per i calcoli "di tutti i giorni" quali il pi greco indicato con
%PI ed il numero di nepero indicato
con %E
Essendo un programma per fare matematica deve esserci una maniera per poter definire varie tipologie di variabili come per esempio per definire liste si usa
makelist(espressione,variabile,valore di partenza, valore finale);
per esempio calcoliamoci il numero di Nepero:
e[n]:=(1+1/n)^n$
Nepero: makelist([x,e[x]],x,1,100),numer$
OPENPLOT_CURVES ([["{plotpoints 1}"], Nepero]);
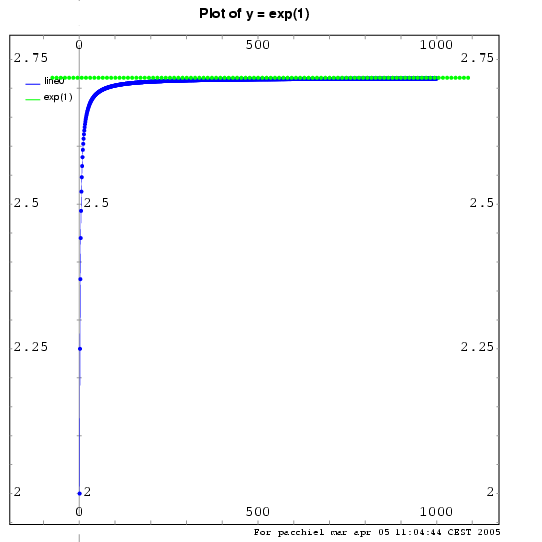
Le funzioni con relative :
- Esponenziale La funzione esponenziale viene chiamata tramite
- Logaritmo
exp( )
e viene rappresentata internamente da %E^x;
le variabili utili per il suo utilizzo sono DEMOIVRE:
che permette di passare ad una rappresentazione trigonometrica
della parte immaginaria di un esponenziale [%E^(%I*b)=COS(b)+%I*SIN(b)],
%ENUMER che insieme ad NUMER
obbliga maxima a esplicitare il valore numerico della espressione
coinvolgente gli esponenziali.
Esiste inoltre %EMODE che permette di semplificare
espressioni del tipo %E^(%I*%PI*X)
Vettori e matrici
Come ogni buon calcolo nel mondo reale spesso capita di dover avere a che fare con operazioni performate su oggetti diversi da meri numeri, ma su oggetti con componenti; per non tirare ancora in ballo i tensori, inziamo a vedere come trattare i vettori e le matrici.Prima di tutto bisogna caricare il pacchetto
vect e poi si possono
effettuare le seguenti operazioni:
- Dot Il prodotto scalare tra vettori si effettua tramite .
- Cross Il prodotto vettoriale si effettua tramite ~, tuttavia sorge il problema di far visualizzare il risultato, per quello si usa
A: [a,b,c];
B: [d,e,f];
C: A~B;
express(C);
[b F - c e, c d - a F, a e - b d]
altrimenti come il sottoscritto vagherete per ore senza meta nel manuale per scoprire il perché.
Equazioni
Una parte importante della matematica riguarda calcoli algebrici e sistemi
(%i7) e1: x^2+y^2-1;
2 2
(%o7) y + x - 1
(%i8) e2: y-x;
(%o8) y - x
(%i9) ALGSYS ([e1,e2],[x,y]);
1 1 1 1
(%o9) [[x = - -------, y = - -------], [x = -------, y = -------]]
SQRT(2) SQRT(2) SQRT(2) SQRT(2)
Analisi
Passiamo alle operazioni proprie dell'analisi:- Limiti
- Derivate
- Integrali integrate(espressione,variabile,);
limit(funzione,variabile,valore,direzione);
diff(espressione,variabile 1,numero di derivate di variabile 1,..., variabile n, numero derivate variabile n);
Equazioni Differenziali
Come ogni buon scienziato so che la natura detta le sue leggi tramite regole differenziali e quindi è buona cosa conoscere come risolvere le cosidette equazioni differenziali, cioè espressioni in cui sono coinvolte derivate di una funzione. Il comando per eseguire questa operazione è ode2(equazione,variabile dipendente,variabile indipendente) ; ecco un esempio:
(%i5) eq:'diff(x,t,2)+a^2*x=0;
2
d x 2
(%o5) --- + a x = 0
2
dt
(%i6) ode2(eq,x,t);
Is a zero or nonzero?
nonzero;
(%o6) x = %K1 SIN(a t) + %K2 COS(a t)
(%i14) ic2(%o6,t=0,x=0,diff(x,t)=A);
A SIN(a t)
(%o14) x = ----------
a
si può vedere l'utilizzo di ic2 che serve per settare
le condizioni iniziali a variabile indipendente fissata
per la variabile dipendente e la sua derivata prima e avere restituiata
la soluzione appropriata (esiste anche ic1 utile per le equazioni di primo ordine).
Plotdf
Magnifico script di Maxima che permette di avere un grafico interattivo di equazioni differenziali del primo ordine. Il grafico che potete vedere nell'immagine grabbata del mio desktop rappresenta il campo delle direzioni nello spazio delle fasi del pendolo con attrito ottenuto con PLOTDF([y,-sin(x)-b*y],[sliders,"b=0:10"],[direction,forward],[trajectory_at,2,0],[xradius,3.2],[nstep,1000]);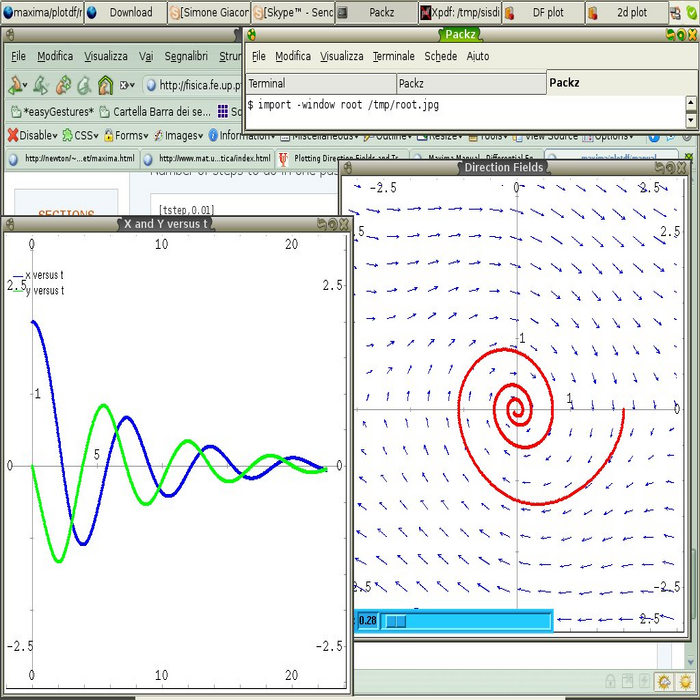
Plotting
Una delle cose che colpisce di più è la capacita di generare grafici e la loro possibile "formattazione" grazie all'interfacciamento con Gnuplot. I principali comandi da questo punto di vista sono:- openplot_curves Primitiva (?) di disegno
- plot2d(espressione,[variabile,valore minimo,valore massimo,opzioni)
- plot3d
SET_PLOT_OPTION ([PLOT_FORMAT, MGNUPLOT]);
come potete vedrere dall'immagine
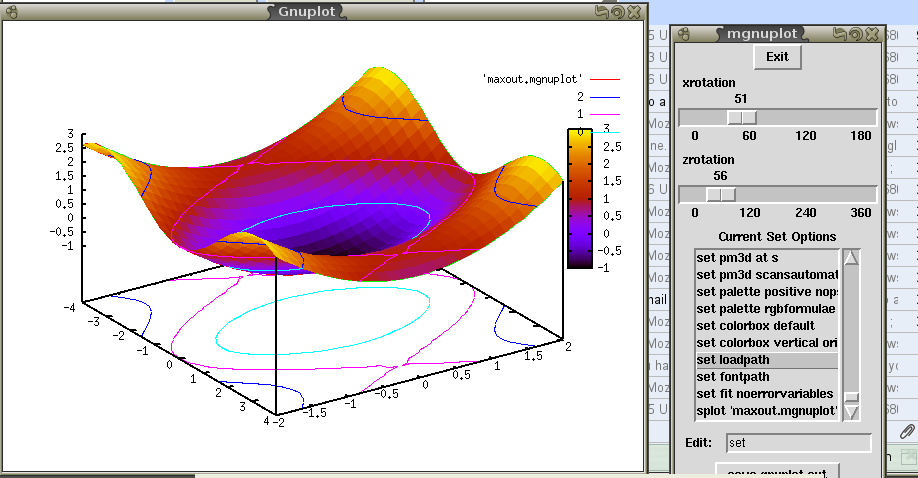
I parametri principali vengono passati tramite opzioni all'interno dei comndi per plottare tramite lo schema [gnuplot_QUALCHECOSA,valore], quelli più importanti sono:
- gnuplot_preamble Inserisce i settaggi iniziali delle opearazioni iniziali di gnuplot; si possono inserire più direttive, basta separarle tramite punto e virgola. Utilissimi
- gnuplot_term Imposta il tipo di terminale: le possibilità per adesso conosco solo ps.
- gnuplot_out_file Va inserita la stringa indicante il nome del file in cui salvare l'output [bisogna per forza impostare assieme il terminale a postscript].
- gnuplot_pm3d Se impostato a 'true' permette di avere la superficie colorata in maniera proporzionale alla altitudo del punto.
set size square oppure set yrange [ymin:ymax]
per ottenere (bisogna usarli assieme pero`!) un grafico con le proporzioni
uguali (utile per grafici polari).
example
plot3d(exp(-x^2-y^2),[x,-5,5],[y,-5,5],[gnuplot_pm3d,true],[gnuplot_preamble,"set hidden3d;set palette gray"]);
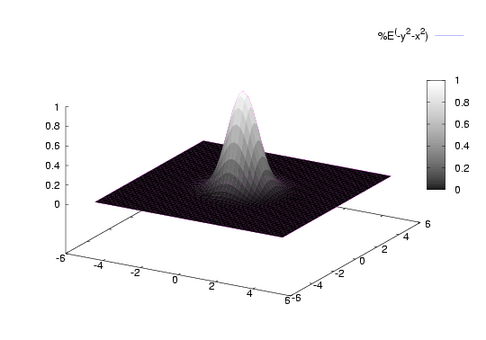
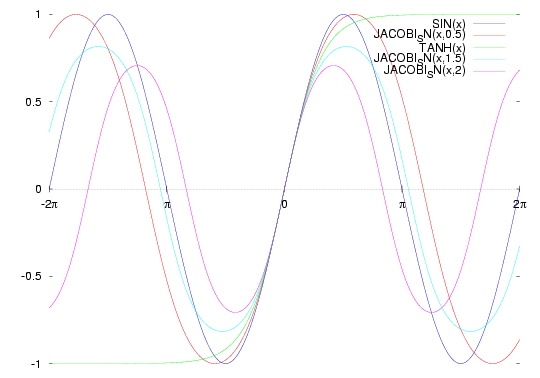
PLOT2D([JACOBI_SN(x,0),JACOBI_SN(x,0.5),JACOBI_SN(x,1),JACOBI_SN(x,1.5),JACOBI_SN(x,2)],
[x,(-2)*%PI,2*%PI],[GNUPLOT_TERM,PS],[GNUPLOT_OUT_FILE,"/tmp/Maxima_plot.ps"],[GNUPLOT_PREAMBLE,"set xtics ('-2{/Symbol p}' -6.283, '0' 0, '2{/Symbol p}' 6.283, '{/Symbol p}' 3.14 , '-{/Symbol p}' -3.14);set xzeroaxis;set xtics axis;unset border"]);
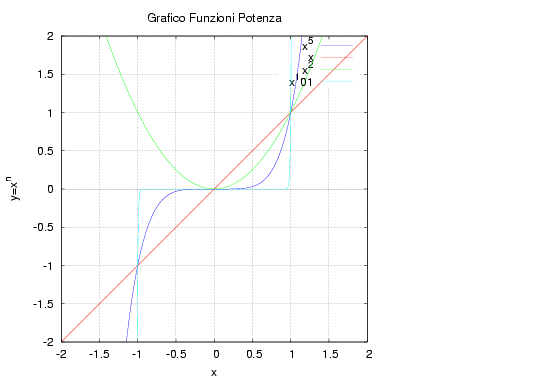
plot2d([x^5,x,x^2,x^101],[x,-2,2],[gnuplot_preamble,"set grid ;set size square;set yrange [-2:2];set xzeroaxis;set title 'Grafico Funzioni Potenza'"]);
Calcolo Tensoriale
Siccome è ancora sotto sviluppo può succedere che i comandi vadano un pó per i fatti loro, eventualmente provate a dare i comandi in maiuscolo
Trovandomi a dover fare spesso calcoli con metriche varie e spazi non banali, risulta utile per me e i miei colleghi avere strumenti a disposizione per avere risultati certi in pocco tempo e Maxima permette tutto ció; il pacchetti ctensor e itensor aggiornati recentemente da Viktor Toth agiscono in cotal senso e permettono di calcolare (una volta data la metrica) tutti i tensori derivanti da essa secondo due filosofie di calcolo: il primo con un lavoro di componenti e il secondo a livello di indici;Ctensor
Prima di tutto caricate il pacchetto in questione con
(i1%) load(ctensor);
(o1%) /path/to/home/.maxima/ctensor.mac
nel caso non sia presente nel vostro sistema scaricatelo da Sourceforge; poi si puó immettere una metrica tramite
(%i2) csetup ();
Enter the dimension of the coordinate system:
2;
Do you wish to change the coordinate names?
n;
Do you want to
1. Enter a new metric?
2. Enter a metric from a file?
3. Approximate a metric with a Taylor series?
volete inserire a mano la metrica della sfera (attenzione che di default lui usa x e y come nomi di coordinate)
e quindi rispondete:
1;
Is the matrix 1. Diagonal 2. Symmetric 3. Antisymmetric 4. General
Answer 1, 2, 3 or 4 :
1;
Row 1 Column 1:
R^2;
Row 2 Column 2:
R^2*sin(x)^2;
Matrix entered.
Enter functional dependencies with DEPENDS or 'N' if none
n;
Do you wish to see the metric?
y;
[ 2 ]
[ R 0 ]
[ ]
[ 2 2 ]
[ 0 R SIN (y) ]
(%o2) DONE
Adesso che abbiamo la metrica possiamo sbizzarirci con tutti quei tensori che sognamo la notte: metrica inversa
(%i4) cmetric (all); Do you wish to see the metric inverse? y; [ 1 ] [ -- 0 ] [ 2 ] [ R ] (%t4) [ ] [ 1 ] [ 0 ---------- ] [ 2 2 ] [ R SIN (y) ] (%o4) DONEL'elenco dei tensori:
- gradiente Esiste quello covariante:grad() e quello controvariante contragrad() che prendono come argomento la funzione di cui fare il (contro-) gradiente e l'array in cui inserire il risultato:
(%i26) depends(f,[x,y]);
(%o26) [f(x, y)]
(%i28) contragrad (f,g); (%o28) DONE (%i29) LISTARRAY (g); f f x y (%o29) [--, ----------] 2 2 2 x x SIN (y)
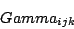 e lcs[i,j,k]=
e lcs[i,j,k]=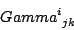
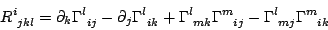 ma si puó anche tentare di calcolare quelli covarianti tramite lriemann(dis)=
ma si puó anche tentare di calcolare quelli covarianti tramite lriemann(dis)=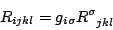 oppure uriemann()
:
oppure uriemann()
:
(%i3) lriemann(all);
2
(%t3) lriem = SIN (y)
2, 2, 1, 1
(%o3) DONE
(%i4) riemann(all);
1
(%t4) riem = - --
1, 2, 1, 2 2
x
2
SIN (y)
(%t5) riem = -------
2, 2, 1, 1 2
x
(%o5) DONE
Itensor
Al contrario del pacchetto sopra esposto, questo lavora a livello indiciale con le quantità tensoriali , ricordo che anche questo si ritrova aggiornato sul CVS di maxima (quando scrivo siamo alla versione 5.9.1).Prima di tutto si dichiara un tensore con entertensor(), viene richiesto il numero di indici covarianti (qualli bassi), controvarianti (quelli alti) e di derivata (nella migliore tradizione tipografica rappresentati dopo una virgola); per esempio
(%i13) ENTERTENSOR ()$ Enter tensor name: n; Enter a list of the covariant indices: [i]; Enter a list of the contravariant indices: [a,b]; Enter a list of the derivative indices: [h]; a b (%t13) n i,he` possibile avere già dei tensori fatti
Ovviamente per gli arditi conoscitori del TeX esiste un comando per espotare espressioni tensoriali in quel linguaggio cosí da poter riportare lunghi scritti nei loro "articoli":
tentex() (da usare avendo caricato preventivamente
il pacchetto omonimo).
Cicli&Programmazione
Le potenzialità di maxima non si limitano ai calcoli, ma come tutti i buoni programmi per computer hanno la capacità di creare cosidetti script in maniera da effettuare calcoli lunghi e perigliosi in automatico; la struttura base è il ciclo for o do che si presenta in tre maniere:
for VARIABILE: VALORE_INIZIALE step INCREMENT thru LIMIT do BODY
for VARIABILE:
da cui prendiamo subito un esempio che ci fa capire la situazione:
(%i1) for i:0 step 1 thru 10 do print("la fattorizzazione di ",i," e` ",factor(i));
che restituisce
la fattorizzazione di 0 e` 0
la fattorizzazione di 1 e` 1
la fattorizzazione di 2 e` 2
la fattorizzazione di 3 e` 3
2
la fattorizzazione di 4 e` 2
la fattorizzazione di 5 e` 5
la fattorizzazione di 6 e` 2 3
la fattorizzazione di 7 e` 7
3
la fattorizzazione di 8 e` 2
2
la fattorizzazione di 9 e` 3
la fattorizzazione di 10 e` 2 5
(%o1) DONE
Ovviamente nulla serveirebbe se non fosse possibile interagire con il sistema:
è possibile richidere di inserire dati da console tramite la direttiva read(expr1,...,expr n) e readonly(expr1,...,exprn)
che aspettano per una immissione di dati da parte dell'utente
come si puó provare con questo script:
limite: read("Inserisci il valore limite della fattorizzazione");
FOR i FROM 0 THRU limite DO PRINT("la fattorizzazione di ",i,"e` ",FACTOR(i))$